Calculating TNT Equivalency for Incident Impulse
Published:
When you are conducting tests on explosives, a common requirement is to determine TNT equivalency. You can determine equivalency using all of the typical blast parameters measured. Peak pressure and impulse are two of the more common methods. Of the two, peak pressure is the simplest.
TNT Equivalency for Peak pressure
Typically we calculate the equivalent peak pressure $\left(E_P\right)$ using,
\[\begin{equation} E_P =\frac{W_{TNT}}{W_{test}}=\left(\frac{Z_{test}}{Z_{TNT}}\right)^3\qquad(1) \end{equation}\]where $Z$ is the scaled distance in $\frac{ft}{lb^{1/3}}$ $\left(\frac{m}{kg^{1/3}}\right)$. This is “easy” because the test explosive pressure is equal to the TNT equivalent of test explosive (a straight line), see Figure 1. You know (it’s your test) the scaled distance of the test explosive $Z_{test}$ and can calculate the $Z_{TNT}$ from the test explosive pressure and the Kingery Bulmash equations. This however is not the case for scaled impulse.
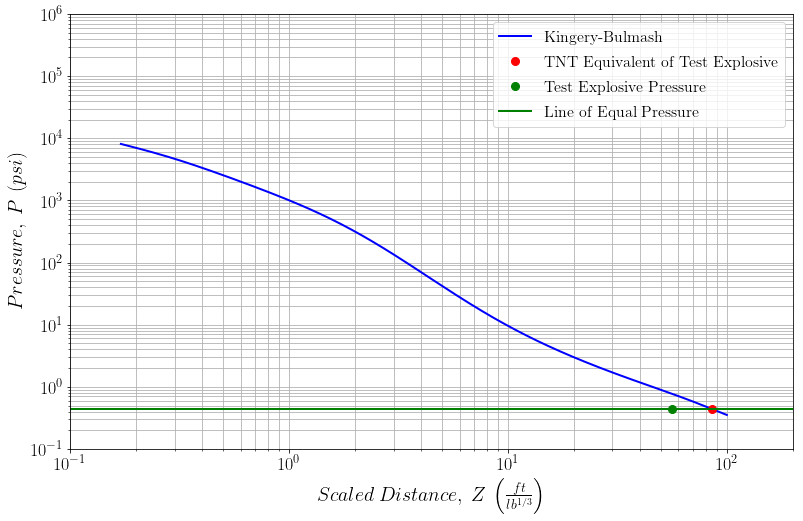
Figure 1 - Plot of pressure vs. scaled distance showing the line of constant pressure. The scaled distance is then read for the “Test Explosive Pressure” and the “TNT Equivalent of Test Explosive”.
TNT Equivalency for Scaled Impulse
To examine TNT equivalency for impulse we need to first calculate the TNT standard, which for most of the world are the Kingery Bulmash equations. I have coded in Python the incident impulse equations below. There are two functions because the equations are only valid over the ranges $0.179 - 2.4:ft$ $\left(0.0674 - 0.955:m\right)$ and $2.4 - 100.0:ft$ $\left(0.955 - 40.0:m\right)$. I currently have a side project as part of my dissertation to code the entire set of equations in python and distribute as a package.
def kingery_bulmash_ii_1(d):
"""
Returns one array
function [incident impulse, distance] = kingery_bulmash_ii_1(d)
kingery_bulmash_ii_1 calculates the Kingery Bulmash incident impulse at
a distance d from from a 1 lb TNT hemispherical surface burst.
incident impulse and distance consists of the impulse in psi-ms and
the distance in feet.
S. Kevin McNeill, 1.0 (Explicitly not copyrighted).
This function is released to the public domain; Any use is allowed.
"""
# Hemispherical Charge
# Incident Impulse Imperial Function 1 (0.170 - 2.41ft)
u_i_ii_f1_h = [0.832468843425, 3.0760329666]
# Incident Impulse Imperial Function 1 (0.170 - 2.41ft)
y_i_ii_f1_h = [1.57159240621, -0.502992763686,
0.171335645235, 0.0450176963051,
-0.0118964626402]
zlog = np.log10(d)
# Incident Impulse - Imperial Function 1 (0.170 - 2.41ft)
u_ii_i1_h = u_i_ii_f1_h[0] + u_i_ii_f1_h[1] * zlog
iii1h = 10**(y_i_ii_f1_h[0] + y_i_ii_f1_h[1] * u_ii_i1_h +
y_i_ii_f1_h[2] * u_ii_i1_h**2 + y_i_ii_f1_h[3] * u_ii_i1_h**3 +
y_i_ii_f1_h[4] * u_ii_i1_h**4)
return iii1h
def kingery_bulmash_ii_2(d):
"""
Returns one array
function [incident impulse, distance] = kingery_bulmash_ii_2(d)
kingery_bulmash_ii calculates the Kingery Bulmash incident impulse at
a distance d from from a 1 lb TNT hemispherical surface burst.
incident impulse and distance consists of the impulse in psi-ms and
the distance in feet.
S. Kevin McNeill, 1.0 (Explicitly not copyrighted).
This function is released to the public domain; Any use is allowed.
"""
# Hemispherical Charge
# Incident Impulse Imperial Function 2 (2.41 - 100ft)
u_i_ii_f2_h = [-2.91358616806, 2.40697745406]
# Incident Impulse Imperial Function 2 (2.41 - 100ft)
y_i_ii_f2_h = [0.719852655584, -0.384519026965,
-0.02601316706301, 0.005957987538,
0.014544526107, -0.00663289334734,
-0.00284189327204, 0.0013644816227]
zlog = np.log10(d)
u_ii_i2_h = u_i_ii_f2_h[0] + u_i_ii_f2_h[1] * zlog
iii2h = 10**(y_i_ii_f2_h[0] + y_i_ii_f2_h[1] * u_ii_i2_h +
y_i_ii_f2_h[2] * u_ii_i2_h**2 + y_i_ii_f2_h[3] * u_ii_i2_h**3 +
y_i_ii_f2_h[4] * u_ii_i2_h**4 + y_i_ii_f2_h[5] * u_ii_i2_h**5 +
y_i_ii_f2_h[6] * u_ii_i2_h**6 + y_i_ii_f2_h[7] * u_ii_i2_h**7)
return iii2h
Why Equal Scaled Impulse is Not a Horizontal Line
Now we need a similar equation to (1) but for impulse. Pressure has a horizontal line of constant pressure with a slope of $0$. Impulse has a line of constant impulse with a slope of $45^\circ$. It is not immediately obvious why this should be so, but with a little algebra we can show why. If we define the scaled impulse as,
\[Y = \frac{I}{W^{1/3}}\] \[I=Y\cdot W^{1/3}\]Then for equal impulses we have,
\[I_{test} = I_{TNT}\] \[Y_{test}\cdot W_{test}^{1/3}=Y_{TNT}\cdot W_{TNT}^{1/3}\]The equivalent impulse from TNT is then,
\[EI=\frac{W_{TNT}^{1/3}}{W_{test}^{1/3}}=\frac{Y_{test}}{Y_{TNT}}\qquad(2)\]We also want the equivalent impulse at the same distance $R$ from the charge,
\[Z=\frac{R}{W^{1/3}}\] \[R=Z\cdot W^{1/3}\] \[R_{test}=R_{TNT}\] \[Z_{test}\cdot W_{test}^{1/3}=Z_{TNT}\cdot W_{TNT}^{1/3}\] \[\frac{W_{TNT}^{1/3}}{W_{test}^{1/3}}=\frac{Z_{test}}{Z_{TNT}}\qquad(3)\]Combining (2) and (3),
\[\frac{Z_{test}}{Y_{test}}=\frac{Z_{TNT}}{Y_{TNT}}\]and taking the logarithm base 10 of both sides we have,
\[log(Z_{test})-log(Y_{test})=log(Z_{TNT})-log(Y_{TNT})\]and rearranging,
\[log(Z_{test})-log(Z_{TNT})=log(Y_{test})-log(Y_{TNT})\] \[\frac{log(Y_{test})-log(Y_{TNT})}{log(Z_{test})-log(Z_{TNT})}=1\]This represents the equation of a 45 degree line from a point $P(Y_{test},Z_{test})$ to a point $P(Y_{TNT},Z_{TNT})$ in the log-log plane. So equivalent impulse is not found with a horizontal line but rather a line with a slope of $1$.
Lines in Log-Log Space
The equation for a straight line in log log space is,
\[y=kx^m\]where m is the slope, $m=\frac{\Delta (log:y)}{\Delta (log:x)}$
and k is the value of $y$ where the line crosses the $x=1$ axis.
Taking the $log_{10}$ of both sides we have,
\[log\:y = m\:log\:(x)+log\:(k)\]solving for $log(k)$
\[log\:(k) = log\:(y) - m\:log\:(x)\]Subsituting our variables for scaled impulse and distance and recalling that $m=1$ we have,
\[log\:(k) = log\:(Y_{test}) - log\:(Z_{test})\]Raising both sides to the power of 10 we have,
\[k=10^{(log\:(Y_{test}) - log\:(Z_{test}))}\]So the equation of the line with slope 1 and running through the point $(Z_{test},Y_{test})$ is,
\[Y_{test}=10^{(log\:(Y_{test}) - log\:(Z_{test}))}\cdot Z_{test}\] \[Y_{test}=k\cdot Z_{test}\]Solving the Kingery Bulmash and Line Equations Simultaneously
The intersection between the Kingery Bulmash curve and the equation of the line with slope 1 and running through the point $(Z_{test},Y_{test})$ will give me the point $(Z_{TNT},Y_{TNT})$. Which can be the used to calculate the Equivalent Impulse, \(EI = \frac{Y_{test}}{Y_{TNT}}\)
So using some recent test data for flash powder we have the following,
# Flash Powder shots 1-3 at 35 ft.
i_test = 0.467268001 #psi-ms measured impulse for flash powder
r_test = 35 #ft - distance to transducer from flash powder charge
w_test = 0.198416 #lb flash powder weight (90 g)
Calculating the scaled impulse for the flash powder we have,
# Scaled Impulse for Test Explosive
# Y = I/W**1/3
y_test = i_test/(w_test)**(1/3)
print(r'The scaled impulse is {:2.4f} psi-ms/lb^1/3.'.format(y_test))
The scaled impulse is 0.8011 psi-ms/lb^1/3.
Calculating the scaled distance for the flash powder we have,
# Scaled Distance for Test Explosive
# Z = R/W**1/3
z_test = r_test/(w_test)**(1/3)
print('The scaled distance is {:2.4f} ft/lb^1/3.'.format(z_test))
The scaled distance is 60.0080 ft/lb^1/3.
The equation for a straight line in log-log space is,
\[y = k\cdot x^m\]where k (y-intercept) is,
\[k=10^{(log(Y_{test})-log(Z_{test}))}\]# Value of the Y Where the Line Crosses the X = 1 Axis
# K = 10**(np.log10(y_test)-np.log10(z_test))
k_test = 10**(np.log10(y_test)-np.log10(z_test))
print('The y-intercept for log-log plot for the explosive under test is {:2.4f} psi-ms/lb^1/3.'.format(k_test))
The y-intercept for log-log plot for the explosive under test is 0.0134 psi-ms/lb^1/3.
To find the point at the intersection between the Kingery Bulmash curve and the equation of the line with slope 1 and running through the point $(Z_{test},Y_{test})$ we need to solve the Kingery Bulmash curve and the line simultaneously,
def equations(p):
# Hemispherical Charge
# Incident Impulse Imperial Function 2 (2.41 - 100ft)
u_i_ii_f2_h = [-2.91358616806, 2.40697745406]
# Incident Impulse Imperial Function 2 (2.41 - 100ft)
y_i_ii_f2_h = [0.719852655584, -0.384519026965,
-0.02601316706301, 0.005957987538,
0.014544526107, -0.00663289334734,
-0.00284189327204, 0.0013644816227]
z, y = p
zlog = np.log10(z)
u_ii_i2_h = u_i_ii_f2_h[0] + u_i_ii_f2_h[1] * zlog
return (10**(y_i_ii_f2_h[0] + y_i_ii_f2_h[1] * u_ii_i2_h +
y_i_ii_f2_h[2] * u_ii_i2_h**2 + y_i_ii_f2_h[3] * u_ii_i2_h**3 +
y_i_ii_f2_h[4] * u_ii_i2_h**4 + y_i_ii_f2_h[5] * u_ii_i2_h**5 +
y_i_ii_f2_h[6] * u_ii_i2_h**6 + y_i_ii_f2_h[7] * u_ii_i2_h**7)-y, k_test*z-y)
x_test_tnt, y_test_tnt = fsolve(equations, (50, 0.4))
print('The TNT equivalent point (Z, Y) is, ({:2.4f}, {:2.4f})'.format(x_test_tnt, y_test_tnt))
The TNT equivalent point (Z, Y) is, (81.8736, 1.0931)
We can then plot the results, see Figure 2,
# Kingery Bulmash Lines
z1 = np.arange(0.17, 2.41, 0.01)
z2 = np.arange(2.41,200, 0.1)
y1 = kingery_bulmash_ii_1(z1)
y2 = kingery_bulmash_ii_2(z2)
# Slope = 1 Line Through Test (z_test, y_test)
z3 = np.arange(1, 200, 0.1)
y3 = k_test*z3
fig, ax = plt.subplots()
ax.loglog(z1,y1, color='blue', label='Kingery-Bulmash')
ax.loglog(z2,y2, color='blue')
ax.loglog(x_test_tnt,y_test_tnt, 'go', label='TNT Equivalent of Test Explosive')
ax.loglog(z3,y3, color='red', label='Line of Equivalent Impulse')
ax.loglog(z_test,y_test, 'ro', label='Test Explosive Point')
ax.grid(True, which="both", ls="-")
ax.legend()
ax.set_xlim(0.1,200)
ax.set_ylim(0.1,1000)
ax.set_xlabel(r'$Scaled\:Distance,\:Z\:\left(\frac{ft}{lb^{1/3}}\right)$')
ax.set_ylabel(r'$Scaled\:Impulse,\:Y\:\left(\frac{psi-ms}{lb^{1/3}}\right)$');
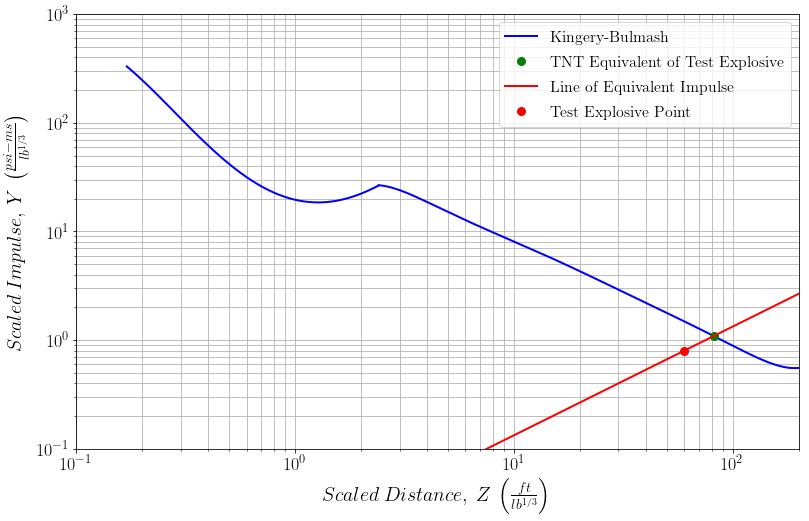
Figure 2 - Plot of scaled impulse vs. scaled distance showing the line of constant impulse. The scaled distance is then read for the “Test Explosive Pressure” and the “TNT Equivalent of Test Explosive”.
Now that we know $Y_{TNT}$ we can calculate the equivalent impulse,
EI = y_test/y_test_tnt
print('The impulse TNT equivalency is {:2.4f}'.format(EI))
The impulse TNT equivalency is 0.7329
The Jupyter Notebook file is available here.

Leave a Comment